Dijkstra's Algorithm - Example
Dijkstra's algorithm is a shortest path search algorithm between a source and all other vertices in a graph without negative weights.
The Algorithm
If you are not yet familiar with Dijkstra’s algorithm, start by looking at the example and its correction. Reading the algorithm first is not the easiest thing.
Function: Dijkstra
Inputs:
- G = (A,S): a digraph without an absorbing cycle.
- p: a function of arity 2
giving the weight of an edge in O(1)
// Example p(1,2) gives the weight of the edge (1,2)
- source: index of the source vertex
Outputs:
- pred: An array containing
for each vertex the chosen
predecessor.
- weight: An array containing
for each vertex the total weight
(the sum of the weights) to traverse
to reach it from the source.
Start:
// Initialization
For $s\in S$:
weight[s] <- inf
preds[s] <- "-"
EndFor
weight[source] <- 0
// Main body of the function
Q <- S
While $Q \neq \emptyset$:
// Start by searching
// minQ, the first vertex to validate
temp <- inf
minQ <- -1
For $q \in Q$:
If weight[q] < temp:
temp <- weight[q]
minQ <- q
EndIf
EndFor
Q <- Q - {minQ}
For each successor q' of q: // Or neighbor if the graph is undirected
// If the recorded distance
// is greater than the distance of the predecessor
// + weight of the edge:
// Update the information of q'
If weight[q'] > weight[q] + p(q,q'):
weight[q'] <- weight[q] + p(q,q')
EndIf
EndFor
EndWhile
End
This algorithm only applies to graphs with positive weights! If your graph contains negative weights (but no negative weight cycles), you can use the Bellman-Ford algorithm.
Example
Here are 2 digraphs (directed graphs).
- Can you use Dijkstra’s algorithm on these graphs to find the shortest path from s to t?
- If so, determine the shortest path from s to t using Dijkstra’s algorithm.
Example 1:
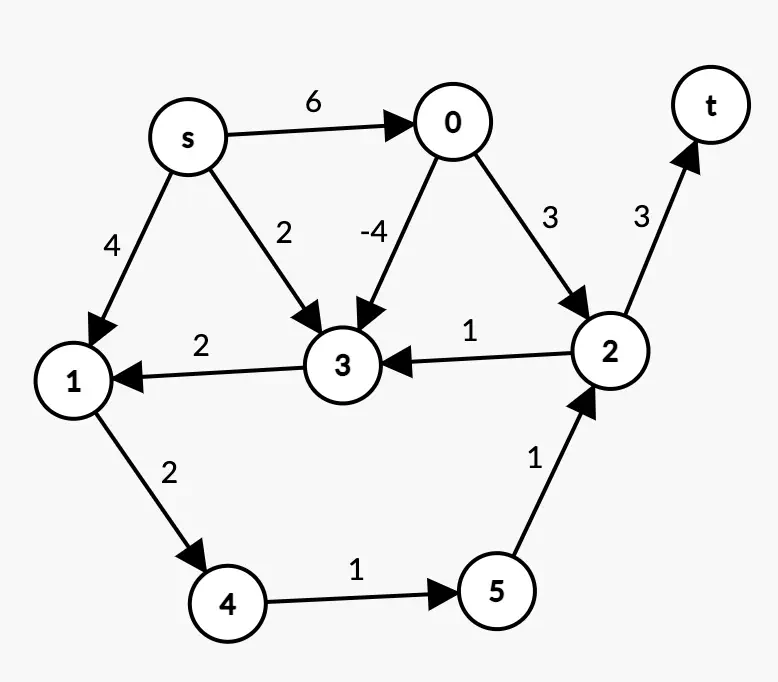
Example 1
Example 2:
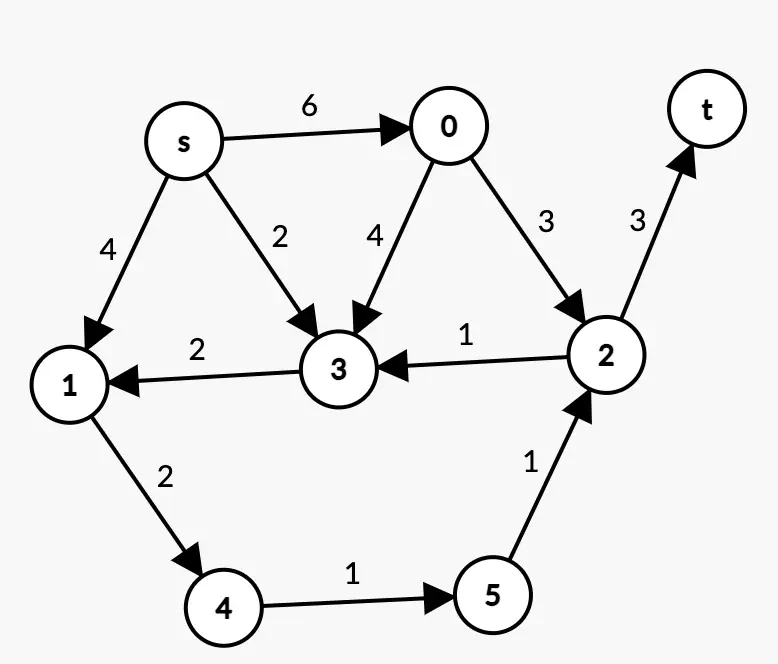
Example 2
Solutions
Solution 1
An edge in the graph is associated with a negative weight. Therefore, Dijkstra’s algorithm does not apply here. You should use the Bellman-Ford algorithm (or another).
Solution 2
You can combine the 2 tables if you prefer, for example by putting in each cell “weight/pred”.
Weight Table
| Steps | s | 0 | 1 | 2 | 3 | 4 | 5 | t |
|---|---|---|---|---|---|---|---|---|
| Init | 0 | $+\infty$ | $+\infty$ | $+\infty$ | $+\infty$ | $+\infty$ | $+\infty$ | $+\infty$ |
| Q -= s | / | 6 | 4 | $+\infty$ | 2 | $+\infty$ | $+\infty$ | $+\infty$ |
| Q -= 3 | / | 6 | 4 | $+\infty$ | / | $+\infty$ | $+\infty$ | $+\infty$ |
| Q -= 1 | / | 6 | / | $+\infty$ | / | 6 | $+\infty$ | $+\infty$ |
| Q -= 0 | / | / | / | 9 | / | 6 | $+\infty$ | $+\infty$ |
| Q -= 4 | / | / | / | 9 | / | / | 7 | $+\infty$ |
| Q -= 5 | / | / | / | 8 | / | / | / | $+\infty$ |
| Q -= 2 | / | / | / | / | / | / | / | 11 |
| Q -= t | / | / | / | / | / | / | / | / |
Some hints to understand this table:
- At each step, we look at the vertex with the smallest associated weight and examine its successors. For example, at the step Q-=s, we look at the successors of s, and if they are closer than our recorded value, then we update the table. For instance, in column 0: 6<$+\infty$.
- “/” is just there for readability. The number above it is the real value of the cell.
- Q -= s means we remove the vertex s from Q. If you look at the algorithm, at the initialization of Q, we have Q = “All vertices”. For each iteration, we deal only with the vertices in Q, so at the step Q -= s, we have filled the column of 0
- Q -= 3 makes no change because among the successors of 3, we have 1. However, weight[1] = 4 which is equal to weight[3] + p(3,1) = 4. We make a change only if the new weight is strictly less than the recorded weight.
- After the step $Q -= 1$, we have 2 vertices of weight 6. The choice doesn’t really matter. Q being a set, it’s unordered, so let’s follow the lexicographic order arbitrarily.
- The table of predecessors below helps keep track of the path taken to reach the vertex. The 2 tables are filled simultaneously.
Predecessors Table
| Steps | s | 0 | 1 | 2 | 3 | 4 | 5 | t |
|---|---|---|---|---|---|---|---|---|
| Init | - | - | - | - | - | - | - | - |
| Q -= s | / | s | s | - | s | - | - | - |
| Q -= 3 | / | s | s | - | / | - | - | - |
| Q -= 1 | / | s | / | - | / | 1 | - | - |
| Q -= 0 | / | / | / | 0 | / | 1 | - | - |
| Q -= 4 | / | / | / | 0 | / | / | 4 | - |
| Q -= 5 | / | / | / | 5 | / | / | / | - |
| Q -= 2 | / | / | / | / | / | / | / | 2 |
| Q -= t | / | / | / | / | / | / | / | / |
Let’s find the shortest path from S to T:
- t’s predecessor is 2
- 2’s predecessor is 5
- 5’s predecessor is 4
- 4’s predecessor is 1
- 1’s predecessor is t
The shortest path from s to t is therefore:
$$s \rightarrow 1 \rightarrow 4 \rightarrow 5 \rightarrow 2 \rightarrow t$$
The total weight is: $4+2+1+1+3 = 11$