Dijkstra's Algorithm - Example
Dijkstra's algorithm is a shortest path search algorithm between a source and all other vertices in a graph without negative weights.

This article has been written by Robin Pourtaud ([email protected]) and published on December 5, 2023.
The content of this article is licensed under CC BY
NC 4.0 : You can freely share and adapt the content for non-commercial purposes as long as you give
appropriate credit and provide a link to the license. In my case, the link to the original article is enough.
Confidentiality if relevant: https://devmath.fr/page/confidentialite/
The Algorithm
If you are not yet familiar with Dijkstra’s algorithm, start by looking at the example and its correction. Reading the algorithm first is not the easiest thing.
Function: Dijkstra
Inputs:
- G = (A,S): a digraph without an absorbing cycle.
- p: a function of arity 2
giving the weight of an edge in O(1)
// Example p(1,2) gives the weight of the edge (1,2)
- source: index of the source vertex
Outputs:
- pred: An array containing
for each vertex the chosen
predecessor.
- weight: An array containing
for each vertex the total weight
(the sum of the weights) to traverse
to reach it from the source.
Start:
// Initialization
For $s\in S$:
weight[s] <- inf
preds[s] <- "-"
EndFor
weight[source] <- 0
// Main body of the function
Q <- S
While $Q \neq \emptyset$:
// Start by searching
// minQ, the first vertex to validate
temp <- inf
minQ <- -1
For $q \in Q$:
If weight[q] < temp:
temp <- weight[q]
minQ <- q
EndIf
EndFor
Q <- Q - {minQ}
For each successor q' of q: // Or neighbor if the graph is undirected
// If the recorded distance
// is greater than the distance of the predecessor
// + weight of the edge:
// Update the information of q'
If weight[q'] > weight[q] + p(q,q'):
weight[q'] <- weight[q] + p(q,q')
EndIf
EndFor
EndWhile
End
This algorithm only applies to graphs with positive weights! If your graph contains negative weights (but no negative weight cycles), you can use the Bellman-Ford algorithm.
Example
Here are 2 digraphs (directed graphs).
- Can you use Dijkstra’s algorithm on these graphs to find the shortest path from s to t?
- If so, determine the shortest path from s to t using Dijkstra’s algorithm.
Example 1:
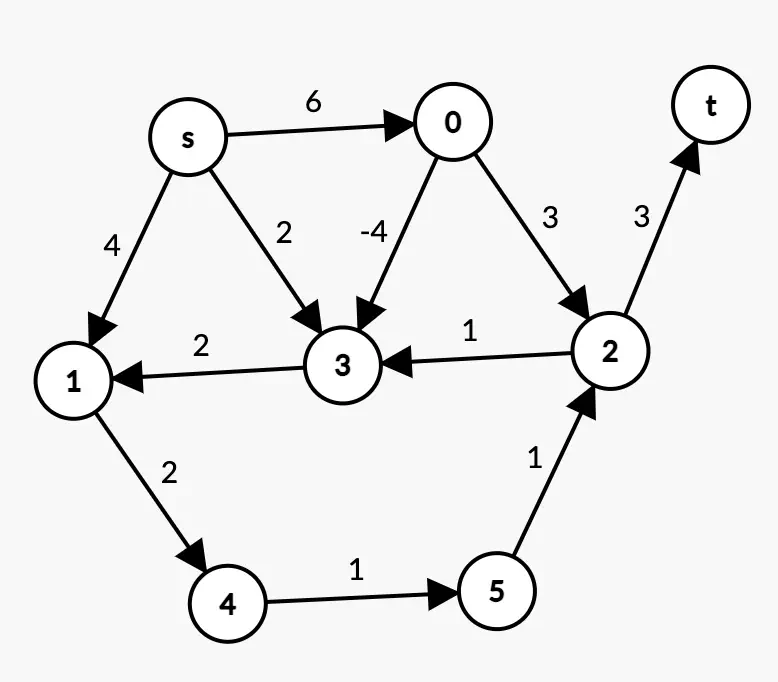
Example 1
Example 2:
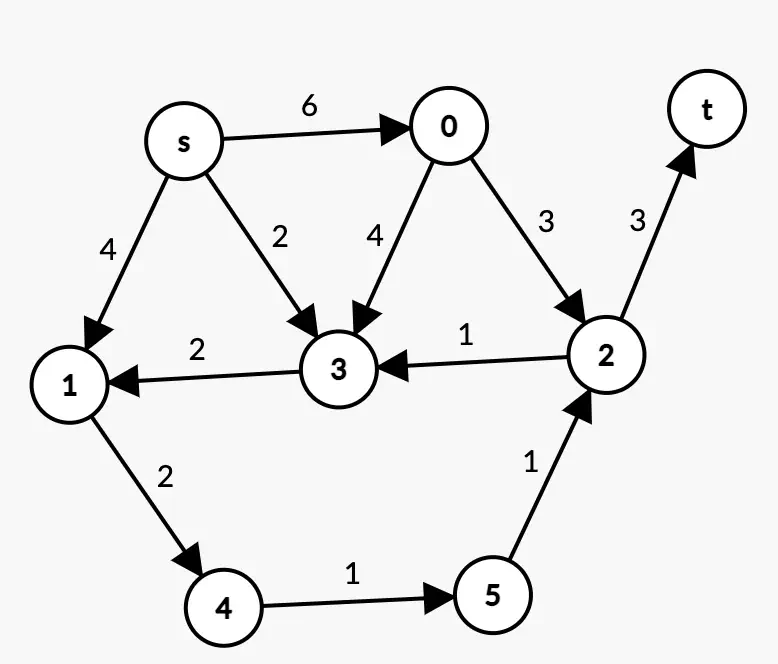
Example 2
Solutions
Solution 1
An edge in the graph is associated with a negative weight. Therefore, Dijkstra’s algorithm does not apply here. You should use the Bellman-Ford algorithm (or another).
Solution 2
You can combine the 2 tables if you prefer, for example by putting in each cell “weight/pred”.
Weight Table
| Steps | s | 0 | 1 | 2 | 3 | 4 | 5 | t |
|---|---|---|---|---|---|---|---|---|
| Init | 0 | $+\infty$ | $+\infty$ | $+\infty$ | $+\infty$ | $+\infty$ | $+\infty$ | $+\infty$ |
| Q -= s | / | 6 | 4 | $+\infty$ | 2 | $+\infty$ | $+\infty$ | $+\infty$ |
| Q -= 3 | / | 6 | 4 | $+\infty$ | / | $+\infty$ | $+\infty$ | $+\infty$ |
| Q -= 1 | / | 6 | / | $+\infty$ | / | 6 | $+\infty$ | $+\infty$ |
| Q -= 0 | / | / | / | 9 | / | 6 | $+\infty$ | $+\infty$ |
| Q -= 4 | / | / | / | 9 | / | / | 7 | $+\infty$ |
| Q -= 5 | / | / | / | 8 | / | / | / | $+\infty$ |
| Q -= 2 | / | / | / | / | / | / | / | 11 |
| Q -= t | / | / | / | / | / | / | / | / |
Some hints to understand this table:
- At each step, we look at the vertex with the smallest associated weight and examine its successors. For example, at the step Q-=s, we look at the successors of s, and if they are closer than our recorded value, then we update the table. For instance, in column 0: 6<$+\infty$.
- “/” is just there for readability. The number above it is the real value of the cell.
- Q -= s means we remove the vertex s from Q. If you look at the algorithm, at the initialization of Q, we have Q = “All vertices”. For each iteration, we deal only with the vertices in Q, so at the step Q -= s, we have filled the column of 0
- Q -= 3 makes no change because among the successors of 3, we have 1. However, weight[1] = 4 which is equal to weight[3] + p(3,1) = 4. We make a change only if the new weight is strictly less than the recorded weight.
- After the step $Q -= 1$, we have 2 vertices of weight 6. The choice doesn’t really matter. Q being a set, it’s unordered, so let’s follow the lexicographic order arbitrarily.
- The table of predecessors below helps keep track of the path taken to reach the vertex. The 2 tables are filled simultaneously.
Predecessors Table
| Steps | s | 0 | 1 | 2 | 3 | 4 | 5 | t |
|---|---|---|---|---|---|---|---|---|
| Init | - | - | - | - | - | - | - | - |
| Q -= s | / | s | s | - | s | - | - | - |
| Q -= 3 | / | s | s | - | / | - | - | - |
| Q -= 1 | / | s | / | - | / | 1 | - | - |
| Q -= 0 | / | / | / | 0 | / | 1 | - | - |
| Q -= 4 | / | / | / | 0 | / | / | 4 | - |
| Q -= 5 | / | / | / | 5 | / | / | / | - |
| Q -= 2 | / | / | / | / | / | / | / | 2 |
| Q -= t | / | / | / | / | / | / | / | / |
Let’s find the shortest path from S to T:
- t’s predecessor is 2
- 2’s predecessor is 5
- 5’s predecessor is 4
- 4’s predecessor is 1
- 1’s predecessor is t
The shortest path from s to t is therefore:
$$s \rightarrow 1 \rightarrow 4 \rightarrow 5 \rightarrow 2 \rightarrow t$$
The total weight is: $4+2+1+1+3 = 11$