ジョンソンのアルゴリズム - 例
ジョンソンのアルゴリズムは、負の重みを持つグラフ内の各頂点間の最短経路を見つけるためのアルゴリズムです。
前提条件
ジョンソンのアルゴリズムの動作を理解するには、他の2つの最短経路アルゴリズムを知っている必要があります:
アルゴリズムのアイデア
- 頂点の追加:グラフ $G$ に頂点 $w$ と、$w$ から $G$ の各頂点への $|V|$ 本の辺を追加します。
- $w$ から $G$ の他のすべての頂点へベルマン-フォードのアルゴリズムを使用します。$d(s)$ は $w$ と $s$ の間の距離を示します。ベルマン-フォードが負のサイクルを検出した場合、アルゴリズムは停止します。
- 頂点 $w$ の削除:この頂点はもはや不要です。ステップ1で追加されたこの頂点とすべての辺を削除します。
- グラフの辺の再加重:グラフ内の各辺 $(u,v)$ に対して、次のように行います:$p((u,v)) := p((u,v)) + d(u) - d(v)$。
- 最短経路の計算:$G$ の各頂点に対して、ダイクストラのアルゴリズムを適用して、すべての頂点間の最短経路を決定します。
**距離が保持されないことに注意が必要です。**辺の重みが $-2$ だった場合、新しい重みは $\geq 0$ になります。しかし、これがポイントではありません。ジョンソンのアルゴリズムは、点 $A$ から点 $B$ への「最短経路」のみを提供します。この経路の重みの合計を取得する必要がある場合は、元のグラフに戻り、ジョンソンによって与えられた経路をたどります。
アルゴリズム / 解答 / 複雑さ
この記事では、ジョンソンのアルゴリズムの適用例のみを紹介しています。ただし、インターネット上で簡単にこの情報を見つけることができます:
例:
負の重みを持つ辺があるグラフ $G$ を考えます。
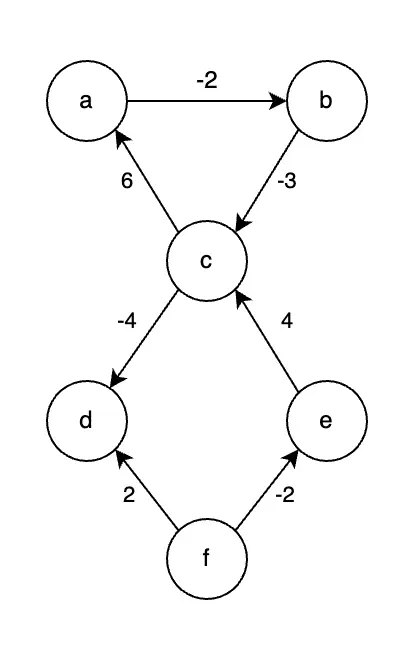
初期グラフ
ステップ1 - 頂点 w の追加
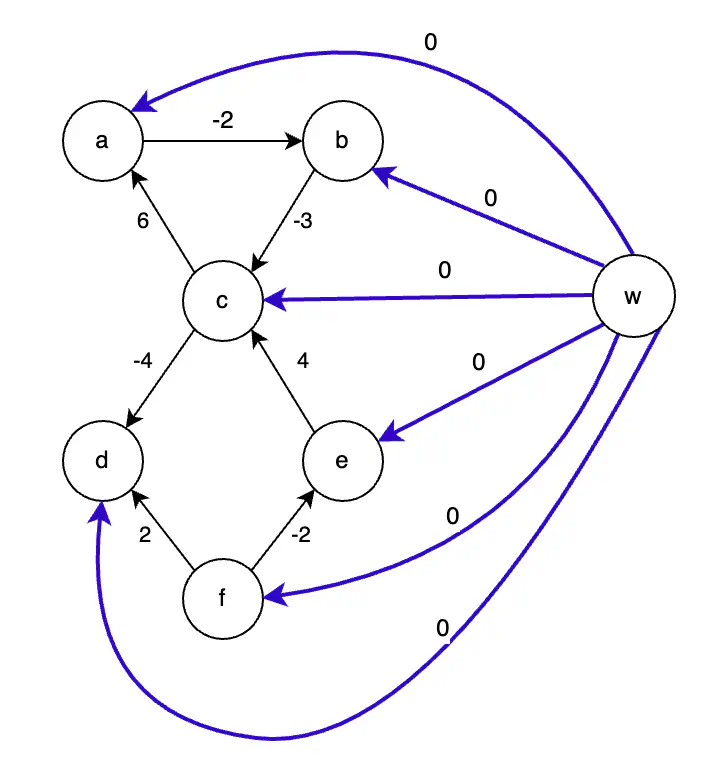
w の追加
ステップ2 - w から他の頂点への最短経路をベルマン-フォードで計算
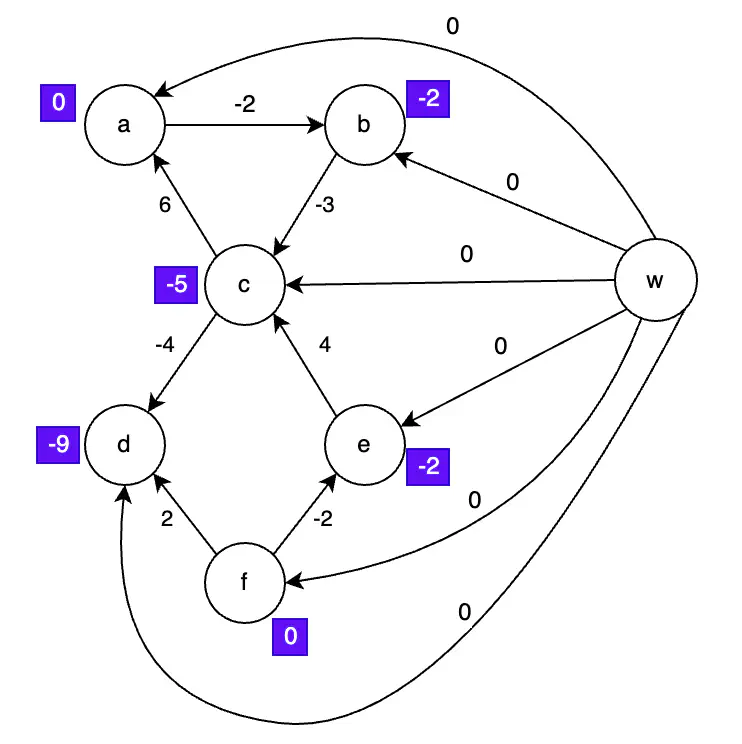
追加された最短経路
ベルマン-フォードのアルゴリズムの結果を紫で示しています。
ステップ3と4 - 辺の再加重
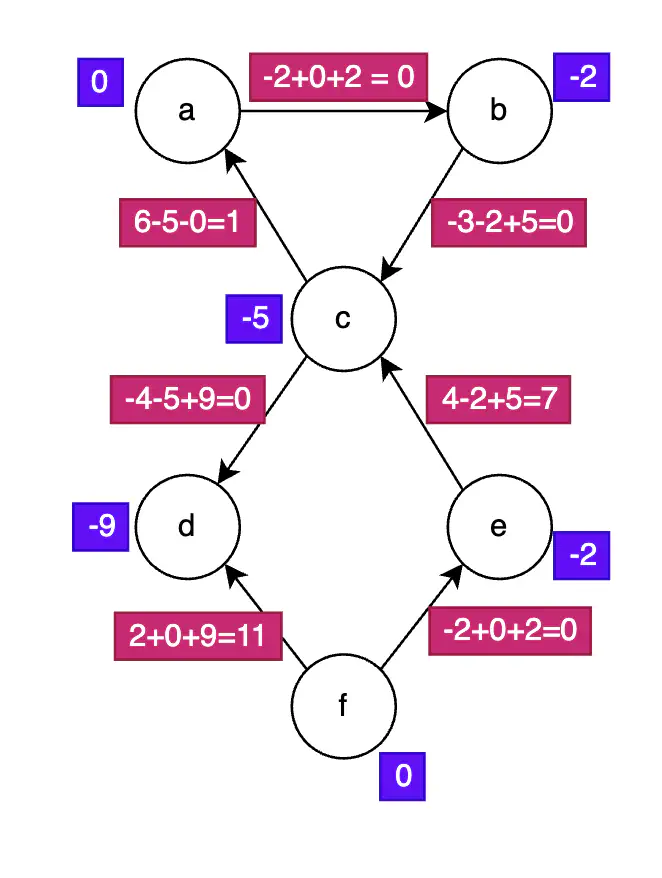
辺の再加重
ステップ5 - すべての辺に対するダイクストラのアルゴリズム
最終的なグラフ $G’$ は以下の通りです:
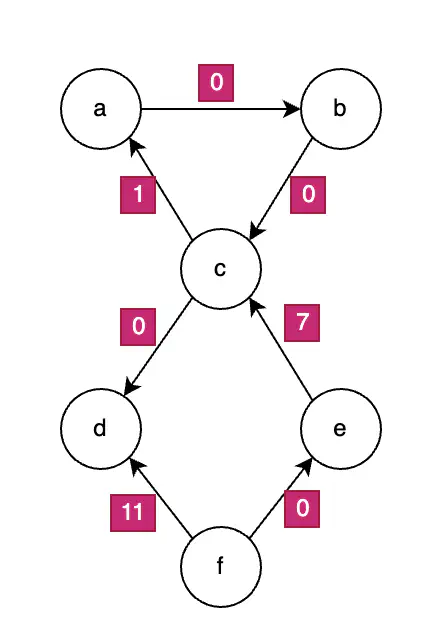
グラフ G'
ステップ5は、ダイクストラのアルゴリズムの単純な適用です。このサイトですでに詳細な使用例があります: ダイクストラのアルゴリズム - 例。
ダイクストラのアルゴリズムから複数の結果を取得するには:
- a から d へ行くには、$a \rightarrow b \rightarrow c \rightarrow d$ の経路を取り、重みは -9(0ではなく、$G$ ではなく $G’$ の重みを使用します)。
- f から d へ行くには、$f \rightarrow e \rightarrow c \rightarrow d$ の経路を取り、重みは -2。
- d から e への経路は存在しません。
残りは読者の演習として残します。