Racine carrée de i
Cet article présente un moyen d'évaluer la racine carrée de i très simplement. Seules des connaissances de base sur les nombres complexes et de la trigonométrie sont nécessaires.
La méthode :
Soit $z=\sqrt{i}$.
- On réécrit z : $z=i^{\frac{1}{2}}$
Cherchons à écrire i en écriture exponentielle :
Nous savons que $e^{i \theta}=cos(\theta)+i sin(\theta)$. Pour obtenir i, il faut donc que $cos(\theta)$ et $sin(\theta)$ soit respectivement égaux à 0 et 1.
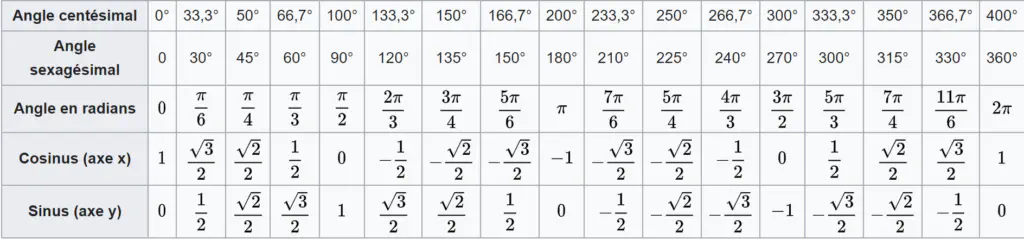
Source : Cercle Trigonométrique - Wikipédia
En utilisant ce tableau, nous pouvons voir qu’un angle de $\frac{\pi}{2}$ serait parfait ! (Utiliser un cercle trigonométrique ou partir de la forme algébrique aurait également été possible pour trouver la forme exponentielle de i).
Cependant, il ne faut pas oublier que cosinus et sinus sont des fonctions périodiques, de période $2 \pi$.
Ce qui nous donne $\forall k \in \mathbb{N}$ : $cos(\frac{\pi}{2}+2k\pi) + i \times sin(\frac{\pi}{2} + 2k\pi) = e^{i \frac{\pi}{2} + 2k\pi} = i$.
Nous pouvons reprendre. En remplaçant i de z, nous avons donc :
$z=i^{\frac{1}{2}} = (e^{i \frac{\pi}{2} + 2k\pi})^\frac{1}{2}$.
Nous pouvons déjà voir qu’en factorisant par 1/2 dans l’exponentielle, et en utilisant une propriété des puissances, nous pouvons obtenir :
$z=(e^{i \frac{\pi}{2} + 2k\pi})^\frac{1}{2}=(e^{\frac{1}{2}(i \pi + 4k\pi)})^\frac{1}{2} = (e^{i \pi + 4k\pi})^\frac{1}{4}) = \sqrt[4]{-1}$
On peut y voir une récurrence… Mais on peut trouver mieux, essayons autre chose !
$z=e^{i\frac{\pi}{4}+ k\pi}$. Avoir “$k\pi$” implique qu’on aura 2 solutions. Si vous avez un doute, regardez un cercle trigonométrique.
$z=e^{i\frac{\pi}{4}+ k\pi}=cos(\frac{\pi}{4}+ k\pi)+i sin(\frac{\pi}{4}+ k\pi)$.
Nous avons donc enfin :
$\frac{\sqrt{2}}{2}+ i \frac{\sqrt{2}}{2}$ ou $-\frac{\sqrt{2}}{2}- i \frac{\sqrt{2}}{2}$.
Ou si vous préférez, en multipliant par $\sqrt{2}$ :
$\frac{1}{\sqrt{2}}+ i \frac{1}{\sqrt{2}}$ ou $-\frac{1}{\sqrt{2}}- i \frac{1}{\sqrt{2}}$.
Une autre méthode :
Vous pouvez trouver un autre moyen de parvenir à la réponse en suivant cette vidéo de Blackpenredpen ici :