Montrer qu'un ensemble est dénombrable
A l'aide d'un exemple, nous allons montrer une méthode classique permettant de démontrer qu'un ensemble est dénombrable.
Définition :
Un ensemble est dit dénombrable s’il existe une bijection (une application bijective) entre cet ensemble et l’ensemble des entiers naturels.
Ici nous utilisons la définition des ensembles dénombrables de Cantor. Nous considérons qu’un ensemble dénombrable est donc infini. Une seconde définition considère qu’il faut montrer qu’il existe une bijection entre une partie de l’ensemble des entiers naturels et cet ensemble.
La méthode
En guise d’exemple, démontrons que $\mathbb{Z}$ est dénombrable.
Exposons une application bijective
Tout d’abord, cherchons instinctivement à associer chaque élément de $\mathbb{Z}$ à $\mathbb{N}$.
Dans notre cas, l’idée est la suivante :
- Les nombres négatifs de $\mathbb{Z}$ correspondent aux nombres impairs de $\mathbb{N}$.
- Les nombres positifs de $\mathbb{Z}$ correspondent aux nombres pairs de $\mathbb{N}$.
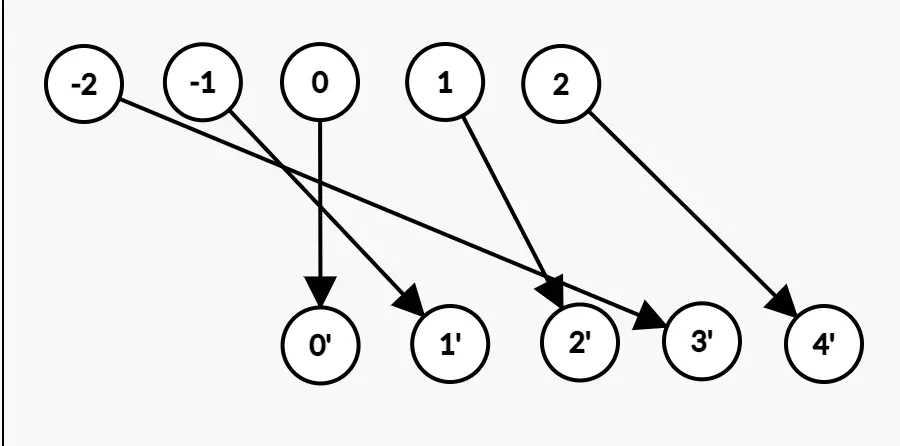
Nous avons donc :
$$f(x) =\begin{cases}2x&\text{si}; x\geq 0\cr-2x-1 &\text{sinon.}\end{cases}$$
Montrons que $f(x)$ est une application bijective de $\mathbb{N}$ dans $\mathbb{Z}$.
Il existe bien sûr d’autres applications bijectives entre $\mathbb{N}$ et $\mathbb{Z}$. Ceci n’est qu’un exemple qui fonctionne.
Montrons que f est une fonction
$f$ est une fonction si tout élément de l’ensemble de départ est associé à, au maximum, un élément de l’ensemble d’arrivée.
Quel que soit le signe de $x$. $f(x)$ est polynomiale de rang 1. $x$ n’a donc qu’une seule image. $f$ est une fonction.
Montrons que f est une application
$f$ est une application si tout élément de l’ensemble de départ possède une image par $f$. Si $f$ est une application, alors son domaine de définition est donc égal à son ensemble de départ.
Le domaine de définition de $f$ est $\mathbb{Z}$.
- $2x$ est défini sur $\mathbb{Z}^+$.
- $-2x-1$ est défini sur $\mathbb{Z}^-$.
Nous avons bien $\mathbb{Z}^+ \cup \mathbb{Z}^- = \mathbb{Z}$. $f$ est une application (car nous avons déja vérifié que $f$ était une fonction).
Montrons que f est injective
$f:X\rightarrow Y$ est une application injective si : $\forall x,y \in X ; (f(x) = f(y) \Rightarrow x = y)$
Nous avons plusieurs cas à prendre en compte :
Si x et y sont positifs : $f(x) = f(y) \Rightarrow 2x = 2y \Rightarrow x = y$ (Injection OK)
Si x et y sont négatifs : $f(x) = f(y) \Rightarrow -2x - 1 = -2y - 1 \Rightarrow x=y$ (Injection OK)
Si x est négatif, y positif (et inversement) : $f(x)= f(y) \Rightarrow -2x-1 = 2y \Rightarrow f(x) \neq f(y)$ (car les nombres impairs et pairs sont disjoints). $f(x)$ ne peut être égale à $f(y)$.
$f$ est donc injective.
Montrons que f est surjective
$f: X \rightarrow Y$ est une application surjective si : $\forall y \in Y ; \exists x \in X ; f(x)=y$
Autrement dit, tout élément de $Y$ possède au moins un antécédent par $f$.
Nous avons bien $\{2n ; | ;n \in \mathbb{Z^+}\}\cup\{-2n-1 ; | ;n \in \mathbb{Z^-}\} = \mathbb{N}$ (se montre trivialement en montrant que la différence entre chaque élément des ensembles “ordonnés” est égale à 1).
$Im(f)=f(\mathbb{Z})=\mathbb{N}$ donc $f$ est donc surjective
Conclusion :
$f$ est bien une application bijective de $\mathbb{Z}$ dans $\mathbb{N}$. $\mathbb{Z}$ est donc dénombrable.