Différences entre fonction et application en mathématiques
Cet article a pour but de mettre en avant la distinction entre une application, fonction et correspondance en mathématiques.
Définition :
Commençons par correctement définir les notions de fonction et application en mathématiques.
Application
Soit $A$ et $B$ deux ensembles. Une application $f$ est un objet qui à tout élément $a\in A$ associe un élément $f(a)$ de $B$.
Plus formellement :
Une relation $R\subseteq A \times B$ est une application si pour tout élément $a$ de $A$ est contenu dans une relation $(a,b)\in R$.
Autrement dit : $R = \{(a,b) \ | \ \forall a \in A \ \exists!b\in B\}$
Pour visualiser tout ça, regardez les exemples à la fin de cet article.
Fonction
Soit $A$ et $B$ deux ensembles. Soit $A’$ un sous-ensemble de $A$. Une fonction $f$ est une relation binaire qui à tout élément $a\in A’$ associe un élément $f(a)$ de $B$.
Plus formellement : Avec $A’ \subseteq A$,
Une relation $R\subseteq A \times B$ est une application si pour tout élément $a$ de $A’$ est contenu dans une relation $(a,b)\in R$.
Autrement dit : $R = \{(a,b) \ | \ \forall a \in A’ \ \exists!b\in B\}$
Ainsi, si $A = A’$, alors cette fonction est une application.
Dans le cas où $f$ associe à au moins un élément plusieurs images (c’est-à-dire que $f$ pointe vers plusieurs éléments distincts à la fois), alors on dira que $f$ n’est pas une fonction, mais une fonction multivaluée ou tout simplement correspondance.
Une correspondance n’est pas une fonction. Pour en savoir plus.
La différence :
La différence n’est pas évidente et cela peut varier énormément selon le contexte. Voici 4 réponses à cette question :
- Synonyme : il sera souvent admis par abus de langage que les deux signifient la même chose. Ce n’est donc pas forcément rigoureux, mais selon votre niveau, la matière sur laquelle vous travaillez, la différence n’aura peut-être pas vraiment d’importance.
- Selon le domaine : sans réfléchir, on réservera souvent le terme “application” en algèbre (“application linéaire” par exemple) et celui de fonction en analyse.
- Historiquement : certains auteurs réservent le terme de fonction dans le cas où $Y$ est un ensemble de nombres entiers comme $\{0,1\}$ par exemple. [2]
- La vraie réponse : si l’ensemble de départ d’une fonction $f$ est égale à son ensemble de définition (appelé aussi domaine), alors $f$ est une application. On dira également que $f$ est bien défini. C’est cette définition qu’on utilisera dans cet article.
En résumé. Une application est une fonction étant elle-même une correspondance. L’inverse n’est pas vrai !
Exemples :
Afin d’illustrer les différences entre fonctions et applications, je vous propose ces diagrammes sagittales suivant :
Exemple 1 :
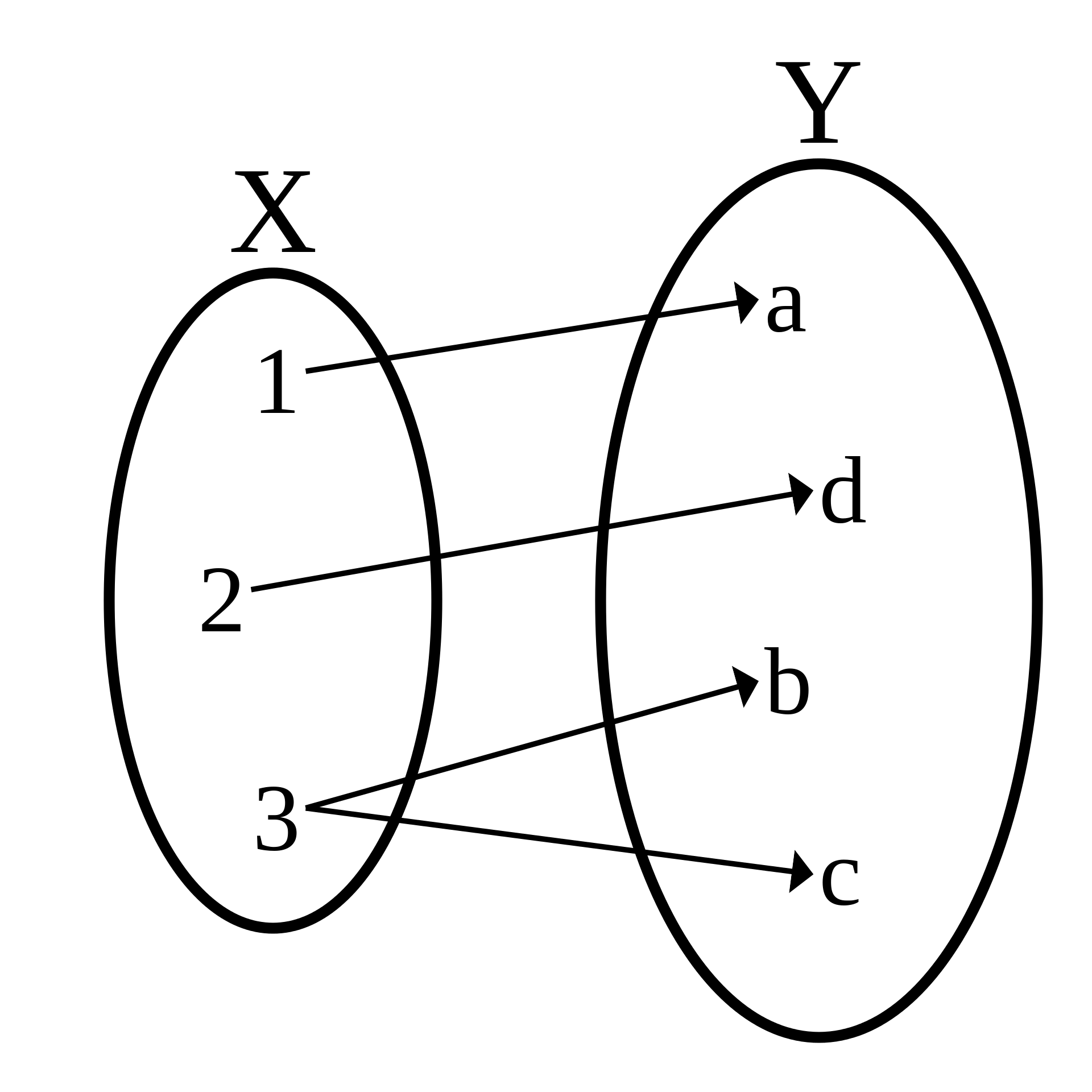
Source Wikipédia
Ceci ne représente ni une application, ni une fonction. $f(3)$ possède plusieurs images, c’est donc seulement une correspondance.
Sans $(3,b)$, ce serait une application.
Sans $(3,b)$ et sans $(3,c)$, ce ne serait plus une application mais seulement une fonction (et une correspondance).
Exemple 2
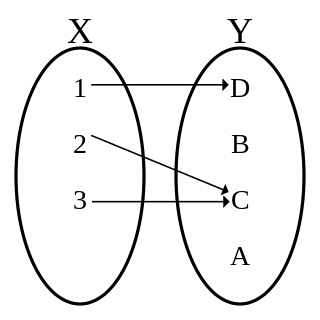
Source Wikipédia
Ceci est une application et donc une fonction. Tout élément de $X$ possède une image par $f$.