Intuition :

6 puissance 1 est 6, 6 puissance 2 36, 6 puissance 3 216. Pour aller plus vite je vous propose ce code python :

for i in range(1,20) : print("6 puissance " + str(i) + " est égale à " + str(6**i))

A l’exécution, nous avons :

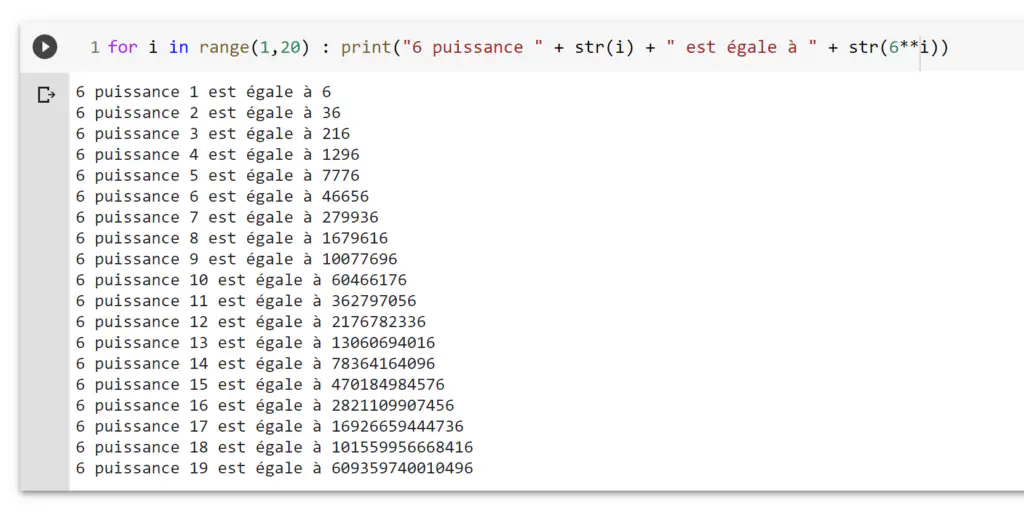
Puissance de 6 de 1 à 19

Bien que très persuasif, ce n’est pas suffisant pour considérer cette propriété comme vraie…

On souhaite que cette propriété soit vraie pour toutes les puissances, une démonstration par récurrence semble donc être un choix judicieux…

Démonstration

Énoncé

Soit $\forall n \in \mathbb{N}\ast$, nous allons prouver par récurrence la propriété $P_n$ : $6^n$ se termine par un 6.

Initialisation

On vérifie que $P_1$ est vrai :

$6^1 = 6$ se termine par un 6.

La propriété est vraie au rang 1.

Hérédité

Soit $n \in \mathbb{N}^\ast$, nous supposons que $6^n$ se termine par un 6.

On peut réécrire notre hypothèse de récurrence comme ceci $\forall k \in \mathbb{N}$ :

$6^n = 10k + 6$

Nous avons donc :

$6^{n+1} = 6 \times (10k + 6)$

$6^{n+1} = 60k + 36$

$6^{n+1} = 60k + 30 + 6$

$6^{n+1} = 10(6k + 3) + 6$

En prenant $k’ = 6k+3$, $k’ \in \mathbb{N}$ :

$6^{n+1} = 10k’ + 6$

Ce qui implique donc que $6^{n+1}$ se termine par un 6.

Conclusion

D’après le principe de récurrence, la propriété $P_n$ est vraie $\forall n \in \mathbb{N}^\ast$.

Aller plus loin

De façon analogue à cette démonstration, vous pouvez prouver cette identité pour les puissances de 5 …