Avec le théorème de Pythagore :

Le théorème :

En géométrie euclidienne, le théorème de pythagore met en relation dans un triangle rectangle, les 2 plus petits cotés avec l’hypothénuse :

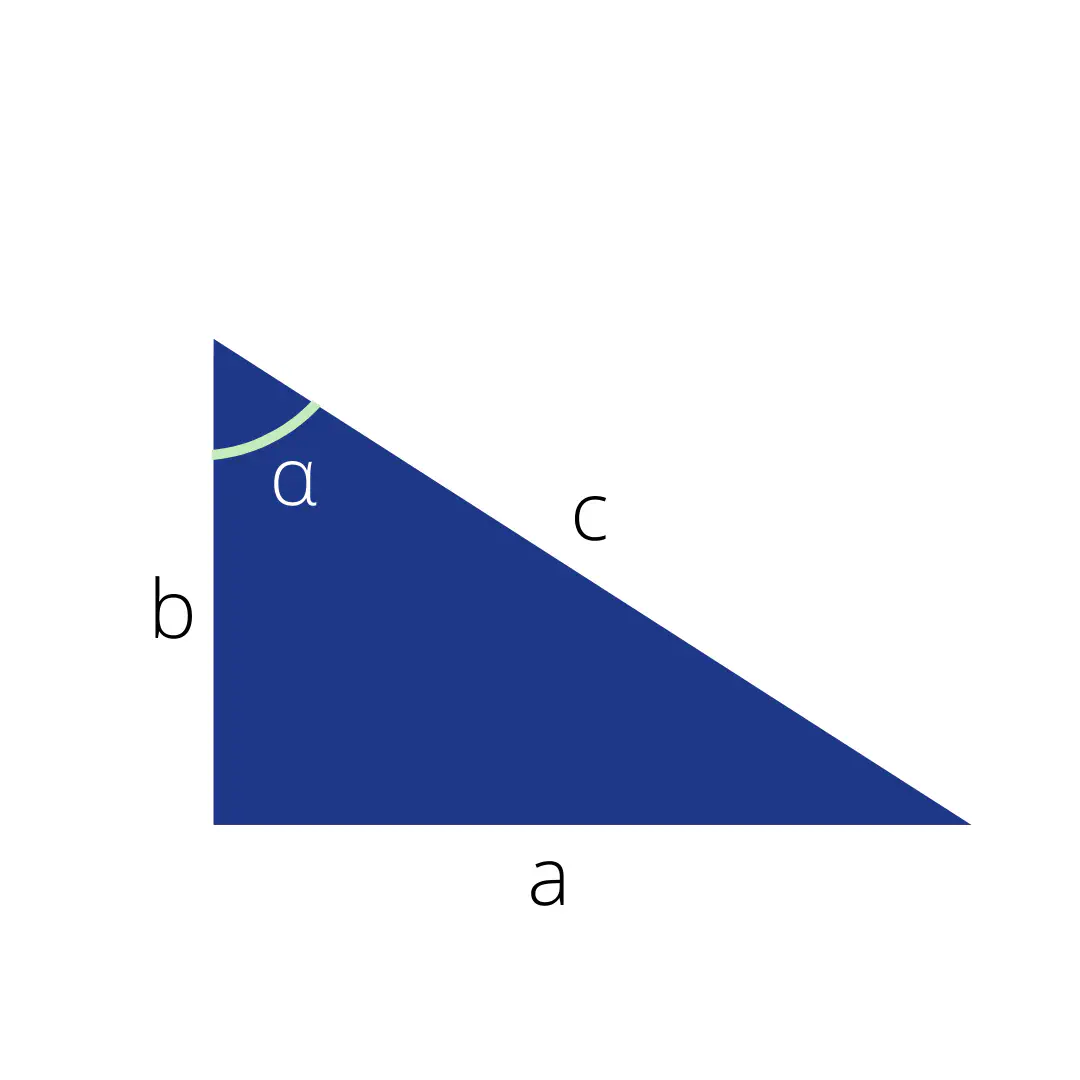
Triangle Rectangle

La célèbre relation est la suivante : $a^2+b^2=c^2$.

Démonstration :

En reprenant les formules vu en 3ème, on a : $\sin \alpha = \frac{a}{c}$ et $\cos \alpha = \frac{b}{c}$

Cela nous donne donc : $a = \sin \alpha \times c$ et $b = \cos \alpha \times c$

En utilisant le théorème de pythagore :

$$a^2+b^2=c^2$$

$$(\sin \alpha \times c) ^2 + (\cos \alpha \times c) ^2= c$$

En prenant $c = 1$, nous obtenons la relation :

$$\sin \alpha ^2 + \cos \alpha ^2 = 1$$

Depuis les formules d’Euler

Les formules :

Soit $\sin \alpha = \frac{e^{i\alpha}-e^{-i\alpha}}{2i}$ et $\cos \alpha = \frac{e^{i\alpha}+e^{-i\alpha}}{2}$

Démonstration :

Reprenons l’équation :

1. $sin \alpha ^2 + \cos \alpha ^2$
2. $= \frac{e^{i\alpha}-e^{-i\alpha}}{2i}^2 + \frac{e^{i\alpha}+e^{-i\alpha}}{2}^2$
3. $= \frac{e^{2i\alpha}-2e^{2i\alpha-2i\alpha}+e^{-2i\alpha}}{-4} + \frac{e^{2i\alpha}+2e^{2i\alpha-2i\alpha}+e^{-2i\alpha}}{4}$
4. $=\frac{2+2}{4}$
5. $=1$