Coefficient binomial (k parmi n)
Cet article présente la notion de coefficient binomial, illustrée d'exemples et d'exercices corrigés. Un niveau de 1ère/Terminale est préférable pour pouvoir suivre cet article. Un rappel sur la notion de factoriel y sera explicité.
Prérequis :
La notion de factorielle est nécessaire pour pouvoir suivre cet article. Noté “!”, la factorielle de n est le produit (usuellement) des entiers naturels de 1 à n. Autrement dit :
$$n! = \Pi_{k=1}^{n}k = 1 \times 2 \times \ldots \times (n-1) \times (n)$$
Pour prendre plusieurs exemples :
- $2! = 1 \times 2$
- $5! = 1 \times 2 \times 3 \times 4 \times 5 = 120$
Pour finir, prenez en compte que $0! = 1$. Vous pouvez en savoir plus ici si vous êtes curieux : Pourquoi 0 factorielle est égale à 1 ? - DevMath
Définition
En dénombrement, on définit le coefficient binomial comme le nombre de parties à “k” éléments dans un ensemble à “n” éléments, “k” et “n” étant des entiers naturels avec k inférieur ou égal à n.
On note le coefficient binomial par la formule :
$$\binom{n}{k} = C^k_n = \frac{n!}{k!(n-k)!}$$
Un ensemble de propriétés faisant intervenir les coefficients binomiaux est trouvable sur Wikipédia.
Exemple
Graphiquement
On retrouve ce coefficient un peu partout en dénombrement, probabilité ou statistique. Pour prendre un exemple, dans le cadre d’une succession d’épreuves de Bernoulli, le coefficient binomial est utilisé pour calculer le nombre de k succès parmi n épreuves.
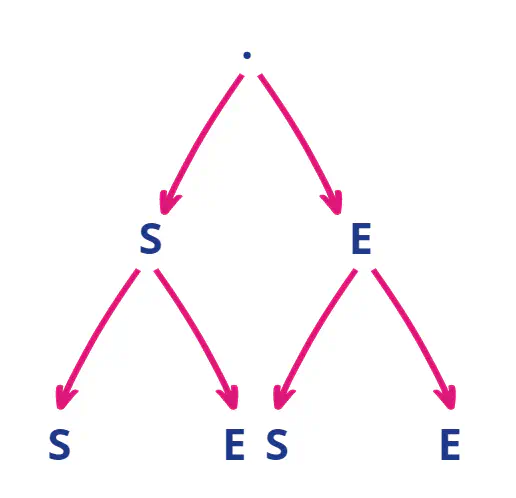
Succession de n épreuves de Bernoulli
Visiblement, selon cette arborescence, il y a :
- 1 façon d’obtenir 2 succès (2 parmi 2 = 1)
- 2 façons d’obtenir 1 succès (1 parmi 2 = 2)
- 1 façon d’obtenir 0 succès (0 parmi 2 = 1)
Cette symétrie dans les résultats se retrouvera bien évidement dans des arborescences plus grandes.
Avec un ensemble
Soit un ensemble $E = \{a,b,c\}$.
Calculons l’ensemble des parties de E : $$\mathcal{P}(E) = \{\varnothing, \{a\}, \{b\}, \{c\}, \{a, b\}, \{a, c\}, \{b, c\}, \{a,b,c\}\}$$
Il y a :
- 1 élément à 0 élément (0 parmi 3 = 1)
- 3 éléments à 1 élément (1 parmi 3 = 3)
- 3 éléments à 2 éléments (2 parmi 3 = 3)
- 1 élément à 3 éléments (3 parmi 3 = 1)
L’ensemble des parties d’un ensemble E a pour cardinal $2^{|E|}$, ce qui correspond à la somme des cardinaux des parties à k éléments. Par exemple, nous avons bien pour cet exemple $1+3+3+1=2^3$. Pour en savoir plus, c’est ici.
Exercices corrigés
Enoncé 1
Un ami me propose de prendre 3 cartes dans un paquet de 52 cartes.
Si j’obtiens le 5, le 6 et le 7 de cœur (sans prendre en compte l’ordre), il a dit qu’il me donnerait 100€.
- Combien y a-t-il de tirages possibles ?
- Quelle est la probabilité d’obtenir ces 100€ ?
Correction 1
Nous voulons obtenir 3 cartes spécifiques parmi un paquet de 52 cartes.
Utilisons la formule !
Avec n = 52 et k = 3, nous obtenons : $\binom{52}{3}$.
Ne calculez pas 52 factorielle “à la main”, 52 factorielle est égale à 8.0658175e+67.
$$\frac{n!}{k!(n-k)!} = \frac{52!}{3!(52-3)!} = \frac{52!}{6(49)!} = \frac{52\times 51 \times 50}{6}= 22100$$
Il y a donc 22100 permutations (mains) différentes.
On veut obtenir une de ces possibilités parmi ces 22100. La probabilité étant à priori uniforme, il y a donc une probabilité de réussite de :
$$\frac{1}{22100}$$
C’est à dire environ 0.004% de chance.
Enoncé 2
Ce même ami me propose maintenant de piocher 3 cartes “une à une” parmi ce même paquet de 52 cartes tout en prenant soin de les remettre dans le paquet à chaque carte. Si j’obtiens 3 cartes identiques, dans ce cas il me donnera 100€.
- Combien y a t-il de mains possibles ?
- Quelle est la probabilité d’obtenir ces 100€ ?
Correction 2
Nous avons à faire à des tirages avec remise. Notre formule ne s’applique pas ici !
Il y a 52 cartes. Il y a $52^3$ tirages possibles !
Il n’y a pas de factorielle en jeu ici. La factorielle est (le plus souvent) utilisé pour calculer le cardinal d’un ensemble de permutations. Autrement dit, la répétition est interdite. Il existe cependant les permutations avec répétitions, mais cela est dans notre cas inutile.
Il y a 52 tirages gagnants dans les $52^3$ tirages. La probabilité (étant uniforme) est donc de $52 \times \frac{1}{52^3}$.
Egalement calculable de la façon suivante : $1 \times \frac{1}{52} \times \frac{1}{52}$. Au premier tour, il y a 100% de chance d’avoir toutes les cartes identiques, au second 1 sur 52, et au troisième 1 sur 52 !
Il faut toujours faire attention si il y a une remise, cela change tout ! Dans ce second énoncé, la notion de factorielle et de coefficient binomial étaient même superflues !