Algorithme de Dijkstra - Exemple
L'algorithme de Dijkstra est un algorithme de recherche de plus court chemin entre une source et tous les autres sommets dans un graphe sans poids négatif.
L’algorithme
Si vous ne connaissez pas encore l’algorithme de Dijkstra, commencez par regarder l’exemple et sa correction. Lire l’algorithme en premier n’est pas la chose la plus simple.
Fonction : Dijkstra
Entrées :
- G = (A,S) : un digraphe sans cycle absorbant.
- p : une fonction d'arité 2
donnant le poids d'un arc $\in O(1)$
// Exemple p(1,2) donne le poid de l'arc (1,2)
- source : index du sommet source
Sorties :
- pred : Un tableau contenant
pour chaque sommet le sommet
précedant choisis.
- poids : Un tableau contenant
pour chaque sommet le poids total
(la somme des poids) à parcourir
pour y accéder à partir de source.
Début :
// Initialisation
Pour $s\in S$ :
poids[s] <- inf
preds[s] <- "-"
FinPour
d[source] <- 0
// Corps de la fonction
Q <- S
TantQue $Q\neq \emptyset$ :
// On commence par chercher
// minQ, le premier sommet à valider
temp <- inf
minQ <- -1
Pour $q \in Q$:
Si poids[q] < temp:
temp <- poids[q]
minQ <- q
FinSi
FinPour
Q <- Q - {minQ}
Pour chaque successeur q' de q : // Ou voisin si graphe non orienté
// Si la distance enregistré
// est supérieur à la distance du prédécesseur
// + poids de l'arc :
// On met à jour les informations de q'
Si poids[q'] > poids[q] + p(q,q'):
poids[q'] <- poids[q] + p(q,q')
FinSi
FinPour
FinTantQue
Fin
Cet algorithme s’applique uniquement sur des graphes de poids positifs ! Si votre graphe contient des poids négatifs (sans circuit de poids négatifs), vous pouvez utiliser l’algorithme de Bellman-Ford.
Exemple
Voici 2 digraphes (graphes orientés).
- Pouvez-vous utiliser l’algorithme de Dijkstra sur ces graphes pour trouver le plus court chemin de s à t.
- Si oui, déterminez le plus court chemin de s à t avec l’algorithme de Dijkstra.
Exemple 1 :
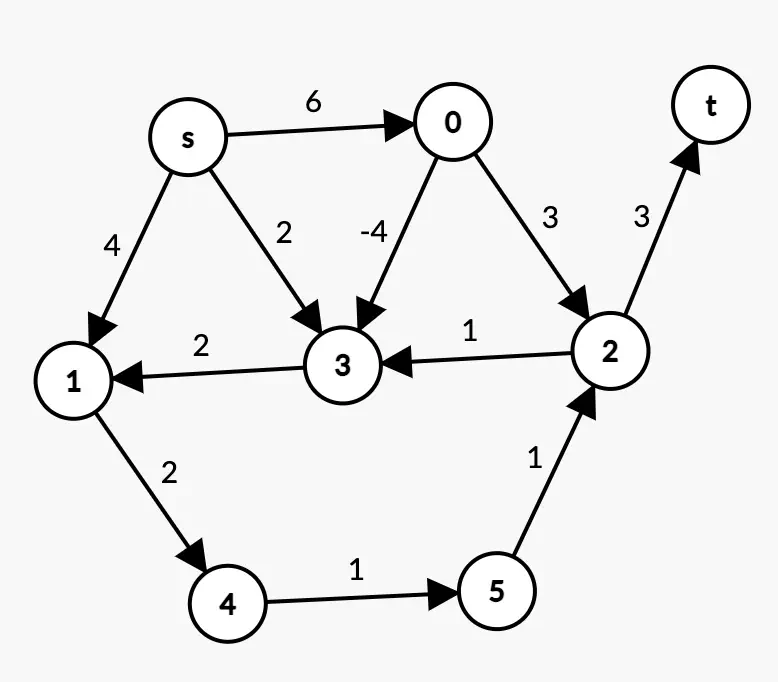
Exemple 1
Exemple 2 :
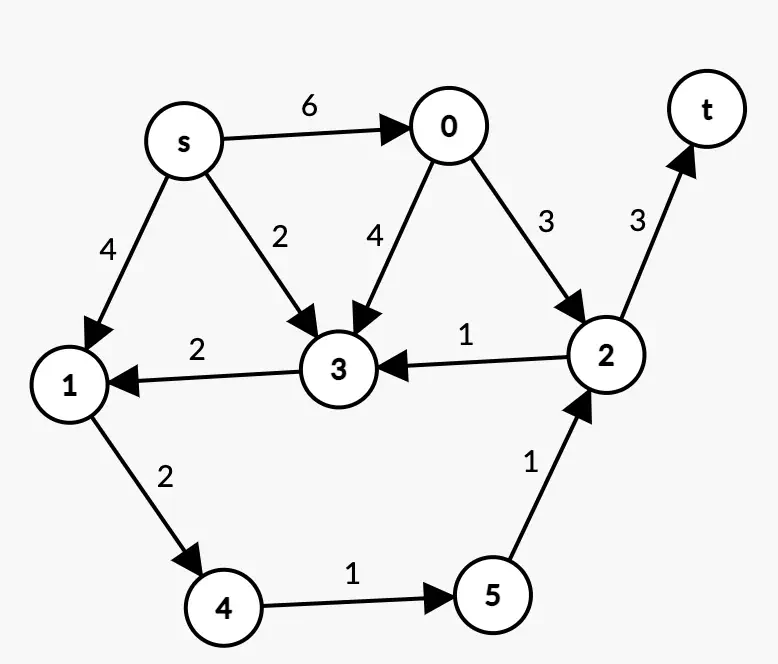
Exemple 2
Solutions
Solution 1
Un arc du graphe est associé à un poids négatif. L’algorithme de Dijkstra ne s’applique donc pas ici. Il faut utiliser l’algorithme de Bellman-Ford (ou autre).
Solution 2
Vous pouvez combiner les 2 tableaux si vous préférez, par exemple en mettant par case “poids/pred”.
Tableau des poids
| Etapes | s | 0 | 1 | 2 | 3 | 4 | 5 | t |
|---|---|---|---|---|---|---|---|---|
| Init | 0 | $+\infty$ | $+\infty$ | $+\infty$ | $+\infty$ | $+\infty$ | $+\infty$ | $+\infty$ |
| Q -= s | / | 6 | 4 | $+\infty$ | 2 | $+\infty$ | $+\infty$ | $+\infty$ |
| Q -= 3 | / | 6 | 4 | $+\infty$ | / | $+\infty$ | $+\infty$ | $+\infty$ |
| Q -= 1 | / | 6 | / | $+\infty$ | / | 6 | $+\infty$ | $+\infty$ |
| Q -= 0 | / | / | / | 9 | / | 6 | $+\infty$ | $+\infty$ |
| Q -= 4 | / | / | / | 9 | / | / | 7 | $+\infty$ |
| Q -= 5 | / | / | / | 8 | / | / | / | $+\infty$ |
| Q -= 2 | / | / | / | / | / | / | / | 11 |
| Q -= t | / | / | / | / | / | / | / | / |
Quelques pistes pour comprendre ce tableau :
- À chaque étape, nous regardons le sommet avec le plus petit poids associé et on regarde ses successeurs. Par exemple, à l’étape Q-=s, nous regardons les successeurs de s, s’ils sont plus proches que notre valeur enregistrée, alors nous actualisons le tableau. Par exemple dans la colonne 0 : 6<$+\infty$ .
- “/” est juste là pour la lisibilité du tableau. Le nombre au dessus est la vraie valeur de la case.
- Q -= s signifie qu’on enlève le sommet s de Q. Si vous regardez l’algorithme, à l’initialisation de Q, nous avons Q = “Tous les sommets”. Pour chaque itération, nous nous occupons uniquement des sommets de Q, si bien qu’à l’étape Q -= s, nous avons remplis la colonne de 0
- Q -=3 ne fait pas de changement car, parmi les successeurs de 3, nous avons 1. Or poids[1] = 4 ce qui est égale à poids[3] + p(3,1) = 4. Nous effectuons une modification uniquement si le nouveau poids est strictement inférieur au poids enregistré.
- Après l’étape $Q -= 1$, nous avons 2 sommets de poids 6. Le choix n’a pas vraiment d’importance. Q étant un ensemble, il n’est pas ordonné, suivons donc arbitrairement l’ordre lexicographique.
- Le tableau des prédécesseurs ci-dessous sert à garder une trâce du chemin parcouru pour arriver au sommet. Les 2 tableaux se remplissent simultanément.
Tableau des prédécesseurs
| Etapes | s | 0 | 1 | 2 | 3 | 4 | 5 | t |
|---|---|---|---|---|---|---|---|---|
| Init | - | - | - | - | - | - | - | - |
| Q -= s | / | s | s | - | s | - | - | - |
| Q -= 3 | / | s | s | - | / | - | - | - |
| Q -= 1 | / | s | / | - | / | 1 | - | - |
| Q -= 0 | / | / | / | 0 | / | 1 | - | - |
| Q -= 4 | / | / | / | 0 | / | / | 4 | - |
| Q -= 5 | / | / | / | 5 | / | / | / | - |
| Q -= 2 | / | / | / | / | / | / | / | 2 |
| Q -= t | / | / | / | / | / | / | / | / |
Cherchons le plus court chemin de S à T :
- t a pour prédécesseur 2
- 2 a pour prédécesseur 5
- 5 a pour prédécesseur 4
- 4 a pour prédécesseur 1
- 1 a pour prédécesseur t
Le plus court chemin de s à t est donc :
$$s \rightarrow 1 \rightarrow 4 \rightarrow 5 \rightarrow 2 \rightarrow t$$
Le poids total est : $4+2+1+1+3 = 11$